R-squared (R^2)(결정계수)
회귀분석을 할 때 R-*squared값 *이라는 것을 많이 들어봤을 겁니다. 이 값이 굉장히 중요하다고 이야기를 하는데 이게 뭔지 제대로 알고 쓰는 경우는 별로 없습니다. 따라서 이번포스팅에서는 R-squared값에 대해 알아 볼 것입니다.
분산
회귀분석에서는 종속변수와 독립변수의 인과관계를 논리적으로 전제하고 독립변수로 종속변수를 설명하는 것이다.
그런데 회귀분석 뿐만아니라 모든 통계는 결국 분산을 얼마나 잘 설명하는지가 목적이다.
즉, 회귀분석이란 종속변수의 분산을 독립변수로 설명하는 과정이다.
따라서 회귀분석은 이론/논리를 통해서 종속변수를 설명할 수 있는 모델을 만들어 종속변수의 분산을 모델(독립변수(들))로 설명한다.
이때 모델(독립변수(들))가 문제가 없다면 종속변수를 모델로 설명하고 남은 오차는 random한 오차이다.
이를 아래와 같은 그림으로 설명할 수 있는데

이때 분산을 얼마나 설명하는지(겹치는 부분)가 R-squared이다.
R-squared = 설명된 분산 / 종속변수의 전체 분산
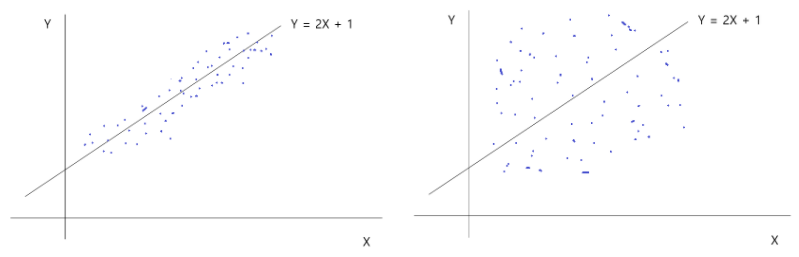
위 예시에서 좌측의 회귀식은 분산의 설명력이 높으며, 우측의 회귀식은 분산의 설명력이 낮은 것이다.
R-squared 공식
위의 그래프의 영역을 SST/SSR/SSE로 설명가능하다.
여기서 SST는 Total Sum of squares로 관측값에서 관측값의 평균을 뺀 결과의 총합, 즉 독립변수 Y의 분산이다.

SSR은 Residual Sum of Squares는 관측값에서 추정값을 뺀 잔차의 총합이며, 에러의 분산(겹치지 않는부분, 설명되지 않는 분산)이다.

SSE는 Explained Sum of Squares로 추정값에서 관측값의 평균을 뺀 결과의 총합이다, 즉 설명되는 분산(겹치는 부분)이다.

따라서 다음과 같은 식도 가능하다.
SST(Y의 총분산) = SSE(설명되는 분산) + SSR(설명 안되는 분산)
(cf. 책에 따라 SSE를 SSR로, SSR을 SSE로 설명하기도 하니 참고바람)
R-squared는 설명된 분산 / 종속변수의 전체 분산이므로 R-squared의 공식은 다음과 같다.

R-squared는 0부터 1까지만 존재하며, R-squared가 0이라면 모델 설명력이 0이며 R-squared가 1이라면 모델 설명력이100%이다.
만약 R-squared가 0.7이면 모델 설명력이 70%라는 것이다.
R-squared의 의미와 단점
R-squared는 모델의 분산 설명력이라고 볼 수 있으며, 모델이 얼마나 데이터를 잘 설명했는지를 의미한다.
하지만 R-squared가 높다고 무조건 좋은 것은 아니다. R-squared가 높더라도 모든 것을 설명하지 못한다.
그 이유는 다음과 같다.
1. R-squared를 확인하기 전에 잔차도(residual plot)가 랜덤하게 분포하는지(분산이 일정한지)를 확인해야 한다.
=> 회귀분석의 가정 중에 하나가 잔차 등분산성이기 때문이다.
CF) 등분산성 : 회귀직선을 중심으로 점들이 위 아래로 퍼진정도가 세로선별로 같음
단순선형회귀분석의 가정 : ysyblog.tistory.com/157
[회귀분석] 단순선형회귀분석(Linear Regression)(1) - 단순선형회귀분석과 가정
회귀분석 회귀분석이란 독립변수(=설명변수)라 불리우는 하나(또는 둘 이상)의 변수에 기초하여 종속변수(=피설명 변수)라 불리우는 다른 한 변수의 값을 설명하고 예측하는 추측통계이다. 상관
ysyblog.tistory.com
2. 의미없는 독립변수의 추가는 R-squared값을 약간이라도 증가시킬 수 있다.
- 하지만 독립변수의 추가는 자유도를 1 증가시키며, 비용이 발생하는 것이다.
3. 높은 R-squared은 과적합 문제로 부터 자유롭지 않다.
- 표본을 수집할 때 마다 R-squared가 다를 가능성이 있다. 만약 표본을 수집할 때마다 R-squared가 들쑥날쑥하다면 그모델은 큰 의미가 없는 것이다.
- 따라서 표본을 랜덤하게 둘로 나누어 한 표본에서 모델을 구축하고 다른 표본에서 모델의 적합성을 다시 테스트해야한다.(Train/Test 데이터 구분)
잔차도(residual plot)

만약 어떤 모델이 위와같은 잔차도를 가질 때, 패턴이 보이지 않는다.

하지만 위 잔차도는 패턴이 있다.(점차 증가함)
이런경우는 회귀분석의 가정을 위반하기 때문에 문제가 있으며 R-**squared가 높다고 하더라도 의미가 없다**.
Adjusted R-squared(수정된 결정계수)
- R-squared는 독립변수가 증가하면 같이 증가하는데 독립변수의 증가는 자유도의 손실이다. 따라서 R-squared의 보정이 필요하다.
- 여기서 보정이란, 추가된 독립변수가 자유도를 잃고도 충분히 분산을 설명했는지를 보는 것이다.
- 즉, 자유도가 감안된 R-squared인 것이며, 이를 Adjusted R-squared이라고한다.
따라서 둘의 크기가 심하게 다르다면 의미없는 독립변수를 넣었다는 의미이다.
Adjusted R-squared의 공식은 다음과 같다.

n은 표본의 수이며 k는 독립변수의 개수이다. 즉 자유도를 감안한 것이다.
결론
R-squared가 높다는 것은 모델의 설명력이 높다는 의미이지만, 독립변수가 증가할 수록 R-squared가 높아질 가능성이 있다. 따라서 AdjustedR-squared를 같이 사용하는 것이 좋다.
또한 R-squared보다 더 중요한 것은 모델에 사용된 독립변수의 논리성/이론적 근거 이다.
해당 포스팅은 아래 유튜브 영상을 참고하여만들었습니다.
'Data Analysis & ML > 회귀분석' 카테고리의 다른 글
| [회귀분석] 단순선형회귀분석(Linear Regression)(9) - 이분산성 (0) | 2021.02.13 |
|---|---|
| [회귀분석] 단순선형회귀분석(Linear Regression)(8) - 더미변수(Dummy Variable) (0) | 2021.02.13 |
| [회귀분석] 단순선형회귀분석(Linear Regression)(6) - 회귀분석과 T-test (2) | 2021.02.13 |
| [회귀분석] 단순선형회귀분석(Linear Regression)(5) - 표준오차 (0) | 2021.02.13 |
| [회귀분석] 단순선형회귀분석(Linear Regression)(4) - 최소제곱추정량(LSE)의 통계적 특성(불편추정량, 효율성, 선형성 가우스-마르코프 정리) (0) | 2021.01.29 |