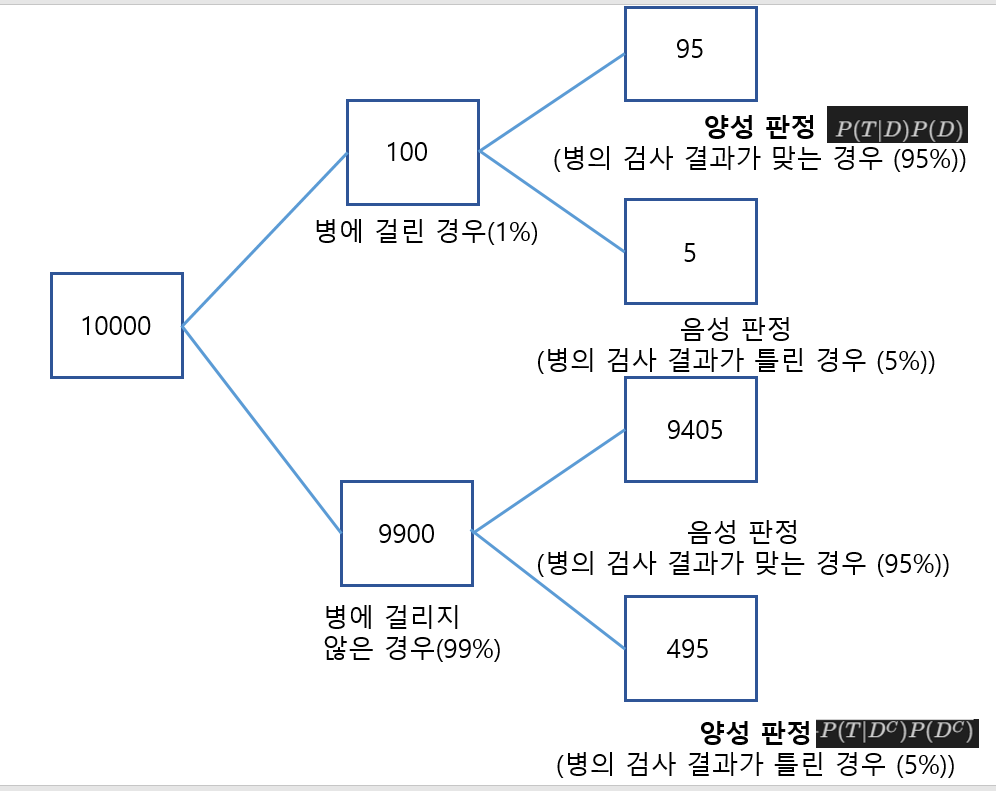
[기초통계학] 독립(Independence)과 조건부확률(Conditional Probability) (1)
독립 (Independence) 정의) 이 성립할 때, 사건 A와 B는 독립이다. 주의하기: 서로소(disjoint) 와 구별하기 – A와 B가 서로소인 사건이라면, A가 발생했을 때 B는 발생할 수 없다. (한편, A와 B가 독립이라면, 사건 A의 발생은 B의 발생여부에 대한 그 어떤 영향도 끼치지 않음) 가 모두 성립할 때, 사건 A, B, C는 독립이다. → 쌍으로 독립(pairwise independence)과 전체 독립 모두 확인해야 A, B, C의 독립을 ..