독립 (Independence)
정의) $P(A \cap B) = P(A)P(B)$이 성립할 때, 사건 A와 B는 독립이다.
주의하기: 서로소(disjoint) 와 구별하기 – A와 B가 서로소인 사건이라면, A가 발생했을 때 B는 발생할 수 없다. (한편, A와 B가 독립이라면, 사건 A의 발생은 B의 발생여부에 대한 그 어떤 영향도 끼치지 않음)
$P(A \cap B) = P(A)P(B)$
$P(B \cap C) = P(B)P(C)$
$P(C \cap A) = P(C)P(A)$
$P(A \cap B \cap C) = P(A)P(B)P(C)$
가 모두 성립할 때, 사건 A, B, C는 독립이다.
→ 쌍으로 독립(pairwise independence)과 전체 독립 모두 확인해야 A, B, C의 독립을 확인할 수 있다.
Newton-Pepys Problem(1693)
- 공정한 주사위를 갖고 있을 때, 다음 중 어떤 경우가 발생할 확률이 가장 높은가?
- a) 6개의 주사위 중에서 적어도 한 개가 ‘6’이 나온 경우
- b) 12개의 주사위 중에서 적어도 두 개가 ‘6’이 나온 경우
- c) 18개의 주사위 중에서 적어도 세 개가 ‘6’이 나온 경우
- 답은 (a)
풀이) ‘적어도 몇 개’ 라는 표현이 나오면 합집합을 생각하기 → 합집합의 여집합은 교집합
⇒ 모든 사건이 독립이기 때문에, 곱셈으로 구할 수 있음!
$ P(A) = 1 - \Large{ (\frac{5}{6}) ^6 }$ ≈0.665 (=1- 6이 한번도 안 나올 확률)
$P(B) = 1-P(B)$ =1− (6이 한 번도 안 나올 확률 + 6이 딱 한 번 나올 확률) (6이 딱 한번 나오는 경우는 12개이므로 12를 곱해준다)
$=1−{\Large ( {\frac {5}{6}) ^{12}} + \frac{1}{6} \times (\frac{5}{6}) ^{11} \times 12}$ ≈0.619
$P(C)$ = 1- (0개, 1개, 2개의 6이나올 확률) (주사위 2개에서 6이 나오는 경우는 ${18\choose 2}$이다)
= $1- {\displaystyle \sum _{k=0} ^{2}} \Large{ {18\choose k}(\frac{1}{6})^k (\frac {5}{6})^{18-k}}$ ≈0.597
(a)가 가장 발생할 확률이 높다.
- 다만 주사위가 공정하다는 것에 기반하지 않다는 것. 각 면이 나올 확률이 같지 않을때는 위 경우가 성립하지 않는다.
조건부 확률 (Conditional Probability)
- 새로운 정보를 얻었을 때, 기존의 ‘믿음/불확실성(uncertainty)’을 어떻게 업데이트하는가?
정의) $P(A|B) = \Large \frac{P(A \cap B)}{P(B)}$ , (P(B) >0이다)
직관적 접근 1) '조약돌 세계관'
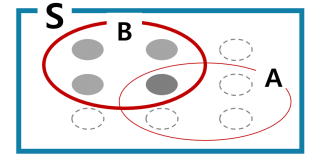
집합 S안에 q개의 조약돌이 있고 이 조약돌 질량의 합이 1이라고 했을때
사건 B에 있는 모든 조약돌을 무시하고 B가 전부라고 여길땨, B안에서도 A도 발생할 확률은 $P(A|B)$ 이다
그런데 B에 있는 질량의 총합이 1이 안되기 때문에 다시 재정규화(renormalize)하는 작업이 필요하다.
따라서 $P(A|B)$에 P(B)를 곱해야한다.
직관적 접근 2) '빈도학파(Frequentist) 세계관'
같은 실험을 무한 번 반복할 수 있다면,

음영표시한 사건 B가 일어난 사건 중, 사건 A 도 같이 일어난 비율
정리
- $P(A \cap B) = P(B)P(A|B) = P(A)P(B|A)$ (곱셈의 교환법칙)
- $P(A_1, A_2, ... A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1,A_2) ... P(A_n| A_1,..., A_{n-1})$ (n 펙토리얼 이론)
- $P(A |B) = \Large \frac {P(B|A)P(A)}{P(B)}$ (베이즈의 정리(Bayes’ Theorem))
'Statistics & Math > 기초통계학' 카테고리의 다른 글
| [기초통계학] Monty Hall(몬티홀) 문제와 Simpson's Paradox(심슨의 역설) (4) | 2023.12.03 |
|---|---|
| [기초통계학] 독립(Independence)과 조건부확률(Conditional Probability)(2) (전체 확률의 법칙, 수형도를 통한 조건부확률의 이해) (0) | 2023.11.05 |
| [기초통계학] 확률의 non-naïve한 정의의 공리, 확률의 특성, 포함배제의 원리 (0) | 2023.10.15 |
| [기초통계학] 확률의 기본 개념(표본공간, 곱의 법칙, 이항정리), 표본추출정리, 확률의 공리 (1) | 2023.10.15 |
| [기초통계학] Two-way ANOVA(이원배치 분산분석)(2) - F-value(F값) 계산 (0) | 2021.02.15 |