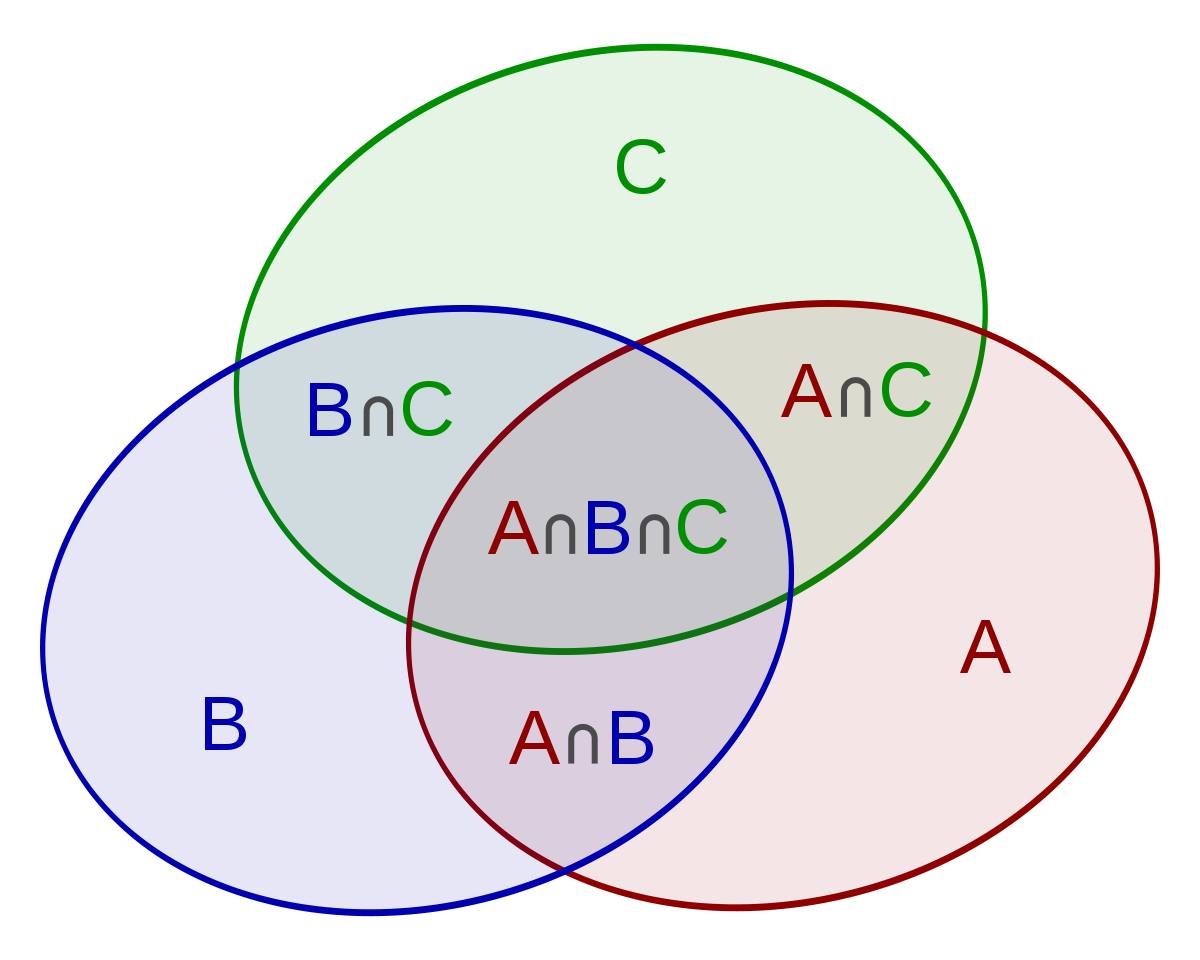
Non-naïve definition of probability 모든 경우의 확률이 각각 다른 경우 확률공간(Probability space) : S와 P로 구성 S : 표본공간 (어떤 사건 A는 S의 부분집합) P : 함수 (어떤 사건 A를 입력으로 하는 함수) 공리 아래 세 가지 공리로부터 대부분의 식을 유도할 수 있음 공집합에 대한 확률은 0이다 (불가능하기 때문에) $P(S) = 1P(ϕ)=0$ 전체 표본 공간의 확률(적어도 사건 A가 발생할 확률)은 1이다. P(S)=1 합사건의 확률은 모든 확률의 합과 같다. (A1, A2.... 가 모두 서로소 일 경우만) $P(\bigcup_{n=1} ^\infty A_n) = \displaystyle\sum_{n=1} ^\infty P(A_n)$ $A_i..

확률론의 활용영역 유전학, 물리학, 계랑경제학, 금융, 역사학, 정치 인문학, 사회과학계에서도 중요도와 활용이 늘어나고 있음 도박과 게임 - 통계에서 여러 번 연구된 주제이다(페르마, 파스칼) 인생 전반: (수학이 활실성에 대한 학문이라면,) 확률은 불확실성(uncertainty)을 계량화하는 것을 가능하게 해 준다. 확률의 기본 개념 표본공간(sample space): 시행에서 발생 가능한 모든 경우의 집합 사건(event): 표본공간의 부분집합 확률의 naïve 한 정의 $P(A) = \frac{(사건 A가 발생하는 경우의 수)}{(발생 가능한 모든 경우의 수)}$ 분모는 표본공간과 같음 두개의 동전을 던졌을 때 둘다 앞면이 나올 확률 : $P(A) = \frac{1}{4}$ 가정 : 모든 경우가 같..

로지스틱이 필요한 이유- 종속변수가 특이할 경우- 종속변수가 이항변수인 경우(변수가 가지는 값이 딱 2가지인 경우)OLS 회귀분석을 쓰면 안되는 이유예제 : 타이타닉, 독립변수 : survived, 종속변수 : pclassimport seaborn as snsimport statsmodels.api as smimport pandas as pdimport numpy as nptitanic = sns.load_dataset("titanic")model1 = sm.OLS.from_formula("survived ~ C(pclass)", data=titanic)result1 = model1.fit()print(result1.summary())1st class의 생존 예측 결과 : 0.62962nd class의 ..

1. [회귀분석] 단순선형회귀분석(Linear Regression)(1) - 단순선형회귀분석과 가정 : ysyblog.tistory.com/157 2. [회귀분석] 단순선형회귀분석(Linear Regression)(2) - 선형회귀분석과 비용함수 : ysyblog.tistory.com/155 3. [회귀분석] 단순선형회귀분석(Linear Regression)(3) - 비용함수의 최소제곱추정량 : ysyblog.tistory.com/156 해당 포스팅은 위 포스팅들에 이어서 진행됩니다. 최소제곱추정량(LSE)의 통계적 특성 최소제곱법에 의해 산출된 최소제곱추정량 W와 b는 확률변수인데 이 확률변수의 평균, 분산, 분포는 어떻게 되고, 추정값이 얼마나 잘 만들어지는지 알아볼 필요가 있다. 특히 최소제곱추정량..