누적분포함수(CDF)
- 주어진 확률변수가 특정 값보다 작거나 같은 확률을 나타내는 함수 (분포를 설명하는 방식)
- '누적'이라는 이름은 특정 값보다 작은 값들의 확률을 모두 누적해서 구한다는 의미에서 붙여진 이름
- '누적분포'함수 이기 때문에 확률변수에 대응하는 모든 확률의 합은 1이 되어야 한다.
- $X \le x$이라는 사건 → 확률을 구할 수 있음
cf) X = 7 -> 사건을 의미 - $F(X) = P(X \le x)$ 이때 F를 누적분포함수라고 지칭
이산확률분포인 경우
- 누적분포함수는 각 확률 질량 함수 값들을 누적하여 계산
- 즉, 확률 변수가 특정 값보다 작거나 같을 확률을 해당 값 이하의 모든 확률질량함수 값의 합으로 계산
- $F(x)=P(X \leq x)= \sum_{i \leq x}P(X=i)$

이산확률변수의 누적분포함수
연속확률분포인 경우
- 누적분포함수는 확률 밀도 함수(Probability Density Function, PDF)의 면적을 통해 계산
- 즉, 확률 변수가 특정 값보다 작거나 같을 확률은 해당 값까지의 확률밀도함수의 면적으로 표현
- $F(x)=P(X \leq x)= \int_{-\infty}^{x} f(t)dt$
-> $\frac{d}{dx}F(x) = f(x)$
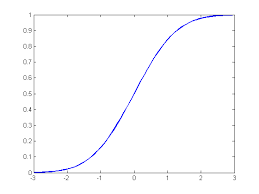
EX) CDF를 이용하여 $P( 1 \le x \le 3)$ 구하기$P(1 < X \le 3) = F(3) - F(1)$
- $\Rightarrow P(a \le X \le b) = F(b) - F(a)$
- $P( X \le 3) = P(X \le 1) + P(1 < X \le 3)$
CDF의 특성 (필요충분조건)
- 증가함수
- 우연속함수 (오른쪽에서 접근하면 연속적임)
- F(X)→0 as X→−∞, F(X)→1 as X→∞
728x90
반응형
'Statistics & Math > 기초통계학' 카테고리의 다른 글
| [기초통계학] 기하분포와 음이항분포 (0) | 2023.12.25 |
|---|---|
| [기초통계학] 기댓값 (Expected Value) (1) | 2023.12.17 |
| [기초통계학] 확률변수 (Random Variable), 베르누이시행, 이항분포 (0) | 2023.12.16 |
| [기초통계학] Gambler's Ruin(도박꾼의 파산) (1) | 2023.12.16 |
| [기초통계학] Monty Hall(몬티홀) 문제와 Simpson's Paradox(심슨의 역설) (4) | 2023.12.03 |