기하확률분포(geometric random variable)
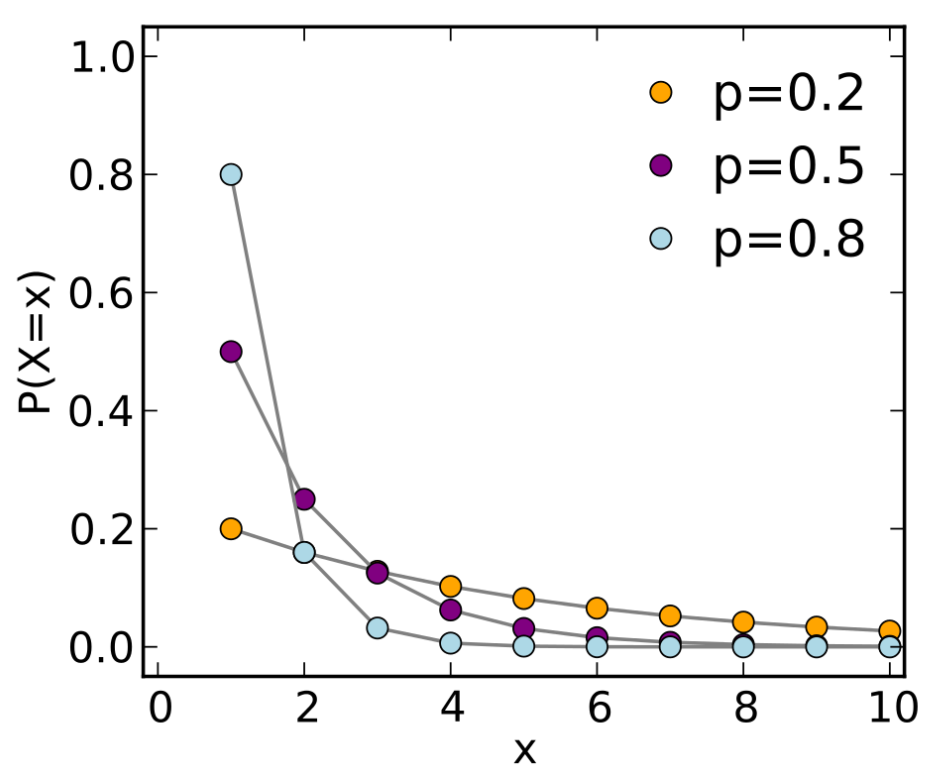
- $ Geom(p)$: 여러 번의 $Bern(p)$ 독립시행에서 첫 번째 성공까지의 실패 수
- 성공전에 얼마나 실패했는지 보여줌
- 이항분포나 초기하분포에서는 시행횟수 n을 정해놓고, 성공한 횟수에 관심을 가졌으나, 기하분포는 시행횟수에 초점을 맞춘것
- 기하분포에서는 X는 성공할때까지 시행했을때 실패한 횟수이며, U는 성공할때까지 시행한 횟수를 의미
- Y = X + 1
- 이런 확률질량함수를 가지는 경우 모수가 p인 기하분포를 따른다고 한다.
$X \sim Geom(p), (q = 1-p)$라고 할 때, - X의 확률질량함수: $P(X = k) = pq^k (k \in { 0,1,...})$
- 조건 확인: $\displaystyle \sum _{k=0} ^\infty pq^k = \frac{p}{1-q} = 1$
- CF) 등비급수의 극한
- $q^k는 등비수열의 합으로 \frac{1}{1-q}로 나타낼 수 있음$
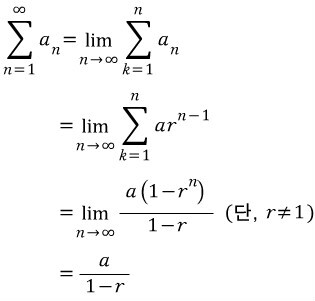
- $q^k는 등비수열의 합으로 \frac{1}{1-q}로 나타낼 수 있음$
- CF) 등비급수의 극한
- 기하분포는 무기억성의 특징이 있음(독립)
- 즉, 4번째까지 실패했을때 5번째 성공확률이나, 5번째까지 실패했을때 6번째의 성공확률이나 모두 p임
기하확률분포의 기댓값
- X는 실패한 횟수, Y는 시행횟수
- E(X) (실패횟수의 기대값)
$E(X) = \displaystyle \sum _{k = 0} ^\infty kpq^k = p \sum _{k = 0} ^\infty kq^k$
$\displaystyle \sum _{k = 0} ^\infty q^k = \frac{1}{1-q}$ → 양쪽에 미분 취하기
$ \displaystyle \sum _{k = 1} ^\infty kq^{k-1} = \frac{1}{(1-q)^2}$
→ $\displaystyle \sum _{k = 1} ^\infty kq^k = \frac{q}{p^2}$
$\therefore E(X) = p\displaystyle \sum _{k = 0} ^\infty kq^k = p \cdot \frac{q}{p^2} = \frac{q}{p}$ - E(Y) (시행횟수의 기대값)
$E(Y) = E(X+1) = \frac{1}{p}$
기하확률분포의 기댓값(Story proof)
$c = E(X)$
$c = 0\cdot p(실패하지 않은경우) + (1+c) \cdot q(첫번째가 실패한경우) = q+cq$
$c = \displaystyle \frac{q}{1-q} = \frac{q}{p}$
음이항분포(Negative Binomial) $NegBin(r,p)$
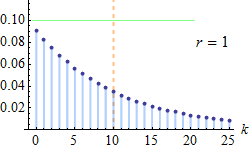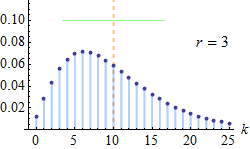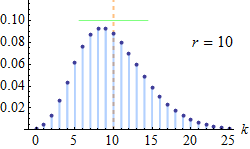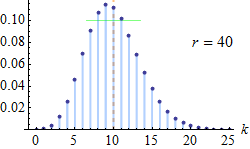
- 음이항분포는 기하분포를 일반화한 분포
- 기하분포는 성공 확률이 p인 베르누이 시행에서 처음으로 성공할 때까지의 시행 횟수
- 반면, 음이항분포는 성공 확률이 p인 베르누이 시행에서 r번째 성공까지의 시행 횟수, 즉, 성공전까지의 실패횟수의 분포
- 음이항확률변수가 크다는 의미는 r번 성공까지 더 많은 시행을 했다는 의미와 같음
- 그렇기에 음이항분포에서는 x번의 시행에서 처음 r-1번의 성공과 마지막 r번째 성공 사이에는 실패가 포함될 수 있음
- 주의 사항 : 음수도 아니고 이항도 아님
- 두개의 변수가 존재 : 모수 r,p
- 여기서는 데구르트 방법을 사용 (기하를 0부터 시작) (1부터 시작하는 거면 성공횟수를 세는것)
1) 의미: 여러 번의 Bern(p) 독립시행 중에서 r번째 성공까지의 실패 횟수
2) PMF: $ P(X = n) = \displaystyle {n+r-1 \choose {r-1}}p^rq^n = \displaystyle {n+r-1 \choose {n}}p^rq^n (n = 0, 1, 2, ...)$
- r-1 : r번 성공하기 전까지의 성공 횟수 (EX 5번째 성공까지의 실패횟수를 구하려면 이전에 4번성공했어야함)
- n : r번 성공하기 전까지의 실패 횟수
- 즉 r번 성공하기 전까지의 성공한 순서/실패 순서(위치)를 정해주면된다
- n + r-1 번 중, r-1번 성공 위치를 선택하는 횟수 = n + r-1 번 중, n번 실패하는 위치를 선택하는 횟수
3) 기대값 구하기 (지시확률변수 활용)
- X는 실패한 횟수, Y는 시행횟수
- E(X) (실패횟수의 기대값)
→ 가장 간단한 상황: r=1일 때 $X \sim Geom(p)$
$E(X) = \Large \frac{q}{p}$
$E(X) = E(X_1 + X_2 + ... + X_r) = E(X_1)+...+E(X_r)$
$X_j$는 j-1번째와 j번째 성공 사이의 실패 횟수라 할 때,
j-1 ~ j 성공 사이의 실패횟수와, j ~ j+1성공사이의 실패횟수는 독립적이며
$X_j \sim Geom(p)$ 이므로
$E(X) = r \times \Large \frac{q}{p}$
- E(Y) (시행횟수의 기대값)
$E(Y) = \frac{r}{p}$
성공분포 (First Success)
- 첫 번째 성공까지 걸린 시도 수 'First Success' 분포: $X \sim FS(p)$
- Y = X -1라 하였을 때(성공 빼기), $Y \sim Geom(p)$
$E(X) = E(Y)+1 = \Large \frac{q}{p} +1= \Large \frac{1}{p}$
이항분포와 음이항분포의 관계
- n번 시행해서 x번 성공할 확률 분포: 이항분포 (cf.https://ysyblog.tistory.com/392)
- r번 성공까지 x번 시행할 확률 분포 : 음이항분포
- 성공확률이 p인 베르누이 시행에서,
- $X \sim Bin(n, p)$ 일 때 n번 시행해서 r번 이상 성공할 확률 $P(X \geq r)$ 와
- $Y \sim NegBin(r, p)$ 일 때 r번 성공하는데 n번 이하 시행할 확률 $P(Y \leq n)$는 같음.
- 즉, $P(X \geq r)=P(Y \leq n)$
예제
- St.Petersburg Paradox
처음으로 동전 앞면이 나올 때까지 동전을 던진 횟수(성공 포함)를 X라 하였을 때, $2^X$달러를 받는 게임이 있다고 하자. 이 게임을 하기 위해 얼마를 내야할까
$Y = 2^X$(받는 돈)
Y의 기대값을 찾는 것이 이문제의 목적
$E(Y) = \displaystyle \sum _{k=1} ^\infty 2^k \cdot \frac{1}{2^k} = \sum _{k=1}^\infty 1 = \infty$ (?..)
∞가 아닌, $2^{40}$ 까지라고 할 때는 $E(Y) = \displaystyle \sum _{k=1} ^{40} 2^k \cdot \frac{1}{2^k} = 40$
$E(Y) = E(2^X) = \infty$
'Statistics & Math > 기초통계학' 카테고리의 다른 글
| [기초통계학] 포아송분포(poisson distribution) (2) | 2023.12.31 |
|---|---|
| [기초통계학] 가설검정과 P값 (p-value) (2) | 2023.12.31 |
| [기초통계학] 기댓값 (Expected Value) (1) | 2023.12.17 |
| [기초통계학] 누적분포함수(Cumulative Distribution Function) (1) | 2023.12.17 |
| [기초통계학] 확률변수 (Random Variable), 베르누이시행, 이항분포 (0) | 2023.12.16 |