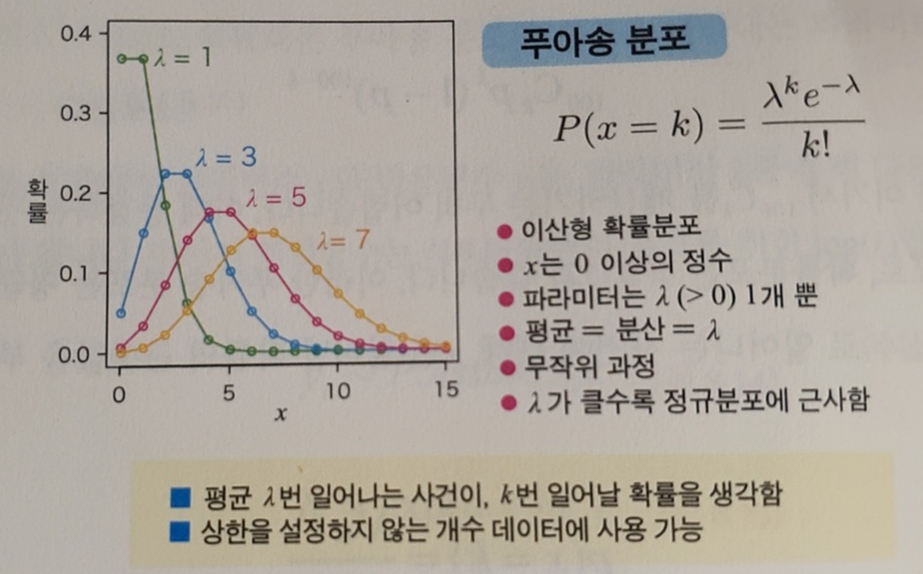
포아송분포(poisson distribution) (푸아송분포)
- 낮은 확률로 일어나는 무작위 사건에 대해 평균이 $\lambda$ 일때 몇 번(k) 일어나는지를 나타내는 확률분포
- ex) 한 시간 동안 오는 이메일의 갯수
- 이항분포의 특수한 경우이며, 시행횟수가 무수히 많아지고 발생확률은 아주 작은 경우
- $X \sim Pois(\lambda)$ 로 표현
포아송 분포 공식 : $P(X=k) = \Large \frac {e^{- \lambda} \lambda^k}{k!}$ $ (k \in {0,1,2,... })$
- 이항분포는 0부터 n까지 k의 범위가 정해져 있지만 포아송에서는 음수가 아닌 모든 정수가 가능함.
- λ는 (속도를 나타내는) 모수(비율모수)로, λ>0 인 상수이다.
- 평균을 나타내며 동시에 분산이기도함. 뜩 평균과 분산이 독립이 아니라는 특징이 있음
- 즉, 평균λ가 커질수록 분포의 넓이도 커짐
- 조건 확인: $\displaystyle \sum _{k=0} ^\infty \frac{e ^{- \lambda} \lambda ^k}{k!} = e ^{-\lambda}e ^{\lambda} = 1$
- $\displaystyle \sum _{k=0} ^\infty \frac{ \lambda ^k}{k!}$ 는 테일러 급수에 따라 $e ^{\lambda}$로 치환된다
- 즉 확률의 합이 1이 되는 것을 확인할 수 있다.
CF) 테일러 급수
f(x)의 테일러 급수는 아래와 같다
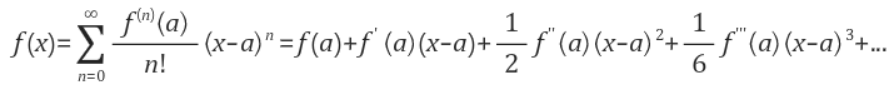
a=0인 경우는 매클로린 급수라고 한다.
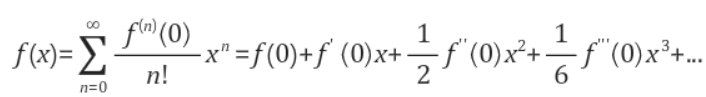
여기서 $e ^{\lambda}$의 매클로린 급수는 아래와 같다
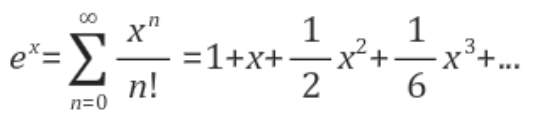
x에 $\lambda$를 대입하면 아래와 같다.
$e ^{\lambda} = \displaystyle \sum _{n=0} ^\infty \frac{ \lambda ^n}{n!}$
포아송분포의 평균
- 기대값은 값과 확률의 곱의 합
- $E(X) = e ^{-\lambda} \displaystyle \sum _{k=0} ^\infty k \frac{ \lambda ^k}{k!}$= $ {\lambda}e ^{-\lambda} \displaystyle \sum _{k=1} ^\infty \frac{ \lambda ^{k-1}}{(k-1)!}$= $ e ^{-\lambda} \displaystyle \sum _{k=1} ^\infty \frac{ \lambda ^k}{(k-1)!}$
- = $ {\lambda} e ^{-\lambda}e ^{\lambda} = {\lambda}$ (테일러 급수 정리활용)
포아송분포의 분산
- $E(X^2) = \displaystyle \sum ^\infty _{k=0} k^2 e^{-\lambda} \lambda^k/k!$$\lambda\displaystyle \sum ^\infty _{k=1} \frac{k\lambda^{k-1}}{k!}$$\displaystyle \sum ^\infty _{k=0} \frac{k^2\lambda^{k-1}}{k!} = \lambda e^\lambda + e^\lambda = e^\lambda (\lambda+1) $
- $= e^{-\lambda}e^{\lambda}(\lambda+1)\lambda = \lambda^2 + \lambda$
- $= \sum^\infty_{k=1} \frac{k\lambda^k}{k!}=\lambda e^\lambda$
- $\displaystyle \sum ^\infty _{k=0} \frac{\lambda^k}{k!} = e^\lambda$
- $Var(X) = E(X^2) -{E(X)}^2 = \lambda^2+ \lambda -\lambda^2 = \lambda$
포아송분포의 활용
- 수를 세는 응용에서 쓰임 (성공의 수를 세는 응용의 수)
- 이항분포처럼 성공은 정의하기 나름이고, 수많은 시도가 기반이 되며 각 시도의 성공확률은 극히 낮아야함
- 예시
1) 한 시간 동안 오는 이메일의 갯수 (수많은 사람이 당신에게 이메일을 보낼 수 있음. 즉 각 사람마다 한시간안에 당신에게 이메일을 보낼 확률은 극히 낮음)
2) 특정 지역에서의 1년간 지진 발생 수
3) 일정 주어진 시간 동안에 도착한 고객의 수
4) 1킬로미터 도로에 있는 흠집의 수
4) 일정 주어진 생산시간 동안 발생하는 불량 수
5) 하룻동안 발생하는 출생자 수
6) 어떤 시간 동안 톨게이트를 통과하는 차량의 수
7) 길바닥에 빗방울이 떨어지는 횟수- 각 사각형에 빗방울이 떨어지는 사건은 이항분포이지만, 그 사건은 서로 독립임.
- 빗방울은 많이 떨어지지만 한 사각형 안에 떨어질 확률은 작기 때문에, 포아송 분포로도 볼 수 있음
- 각 사각형에 빗방울이 떨어지는 사건은 이항분포이지만, 그 사건은 서로 독립임.
- 위 예시들은 완벽한 포아송 분포가 아니지만 추정하기 유용한 분포임
포아송근사(poisson approximation)
- poisson paradigm이라고도 부름
- 어떤 큰 숫자 n에 대하여 $A_1, ..., A_n$의 사건들이 각각 $P(A_j) = p_j$라는 낮은 확률로 발생하고, 각 사건은 독립(이거나 weakly dependent)일 때, 발생하는 사건($A_j$)의 수는 $Pois(\lambda)$의 분포를 따른다.
- $\lambda = \sum p_j$
- 또한 $\sim Bin(n,p)$ 는 n→∞ , p→0 하고 np=λ 가 상수로 유지될 때 (n과 p가 증가하는 속도가 같음) 이항확률변수 X의 분포는 포아송에 근사하게 된다.
- 증명)
$P(X = k) = \displaystyle {n \choose k}p^k(1-p)^{n-k}$이고 $p = \Large \frac {\lambda}{n}$로 놓았을 때,
= $\displaystyle \frac {n(n-1)...(n-k+1)}{k!} \cdot (\frac{\lambda}{n})^k \cdot (1- \frac{\lambda}{n} ) ^{n-k}$
= $\displaystyle \frac{n(n-1)...(n-k+1)\lambda^k}{k!n^k} \cdot (1-\frac{\lambda}{n})^n \cdot (1-\frac{\lambda}{n})^{-k}$$\displaystyle \frac{n(n-1)...(n-k+1)}{n^k} \rightarrow 1, (1- \displaystyle \frac{\lambda}{n})^{-k} \rightarrow 1, \displaystyle (1- \frac{\lambda}{n})^n \rightarrow e^{-\lambda}$ 이므로 - $\Rightarrow P(X= k) \rightarrow \displaystyle \frac{\lambda^k}{k!}\cdot e^{-\lambda}$
- 이고 n→∞ 에 따라$\Rightarrow P(X= k) \rightarrow \displaystyle \frac{\lambda^k}{k!}\cdot e^{-\lambda}$
- $\displaystyle \frac{n(n-1)...(n-k+1)}{n^k} \rightarrow 1, (1- \displaystyle \frac{\lambda}{n})^{-k} \rightarrow 1, \displaystyle (1- \frac{\lambda}{n})^n \rightarrow e^{-\lambda}$ 이므로
728x90
반응형
'Statistics & Math > 기초통계학' 카테고리의 다른 글
| [기초통계학] 지수분포(지수분포의 기댓값과 분산,지수분포의 무기억성) (0) | 2024.02.18 |
|---|---|
| [기초통계학] 확률밀도함수 (연속확률분포, 균등분포) (1) | 2024.01.06 |
| [기초통계학] 가설검정과 P값 (p-value) (2) | 2023.12.31 |
| [기초통계학] 기하분포와 음이항분포 (0) | 2023.12.25 |
| [기초통계학] 기댓값 (Expected Value) (1) | 2023.12.17 |